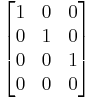
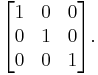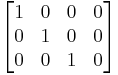Main diagonal
In linear algebra, the main diagonal (sometimes leading diagonal or major diagonal or primary diagonal or principal diagonal) of a matrix  is the collection of entries
is the collection of entries 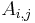 where
where  is equal to
is equal to  .
.
The main diagonal of a square matrix is the diagonal which runs from the top left corner to the bottom right corner. For example, the following matrix has 1s down its main diagonal:
A square matrix like the above in which the entries outside the main diagonal are all zero is called a diagonal matrix. The sum of the entries on the main diagonal of a square matrix is known as the trace of that matrix.
The main diagonal of a rectangular matrix is the diagonal which runs from the top left corner and steps down and right, until the right edge or the bottom edge is reached.
The diagonal of a square matrix from the top right to the bottom left corner is called antidiagonal, counterdiagonal, secondary diagonal, or minor diagonal.
References
- Weisstein, Eric W., "Main diagonal" from MathWorld.
- Main diagonal in Mathwords